为什么 pyplot.contour() 要求 Z 是一个二维数组？

问题描述：

该matplotlib.pyplot.contour()函数接受 3 个输入数组X，Y和Z。

数组X和Y指定点的 x 和 y 坐标，而Z指定在点处评估的感兴趣函数的对应值。

我理解，这样np.meshgrid()可以很容易地生成作为参数的数组contour()：

X = np.arange(0,5,0.01)
Y = np.arange(0,3,0.01)

X_grid, Y_grid = np.meshgrid(X,Y)
Z_grid = X_grid**2 + Y_grid**2

plt.contour(X_grid, Y_grid, Z_grid)  # Works fine

这很好用。而且方便的是，这也很好用：

plt.contour(X, Y, Z_grid)  # Works fine too

但是，为什么要求Z输入是二维数组？

为什么如下操作不允许，即使它指定所有相同的数据均已适当对齐？

plt.contour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel())  # Disallowed

此外，当仅 Z指定（没有相应的X和）时，语义是什么Y？

解决方案 1：

查看文档contour发现有几种方法可以调用此函数，例如contour(Z)或contour(X,Y,Z)。因此，您会发现它根本不需要存在任何X或值。Y

但是，为了绘制轮廓，函数必须知道底层网格。Matplotlibcontour基于矩形网格。但即便如此，如果允许contour(z)为z1D 数组，则无法知道应如何绘制场。在 为 2D 数组的情况下contour(Z)，Z其形状明确地设置了绘图的网格。

X一旦知道了网格，可选和数组是否被展平就变得不重要了Y；这实际上就是文档告诉我们的：

X 和 Y 必须都是二维的，并且与 Z 形状相同，或者它们必须都是一维的，这样 len(X) 是 Z 中的列数，len(Y) 是 Z 中的行数。

类似的东西显然
plt.contour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel())无法生成等高线图，因为有关网格形状的所有信息都丢失了，而且等高线函数无法知道如何解释数据。例如，如果len(Z_grid.ravel()) == 12，底层网格的形状可以是 中的任何一个(1,12), (2,6), (3,4), (4,3), (6,2), (12,1)。

当然，一种可能的解决方法是允许使用一维数组并引入参数shape，例如plt.contour(x,y,z, shape=(6,2))。然而事实并非如此，所以你必须接受Z需要是二维的事实。

但是，如果您正在寻找一种方法来获取具有扁平（散开）阵列的等高线图，则可以使用plt.tricontour()。

plt.tricontour(X_grid.ravel(), Y_grid.ravel(), Z_grid.ravel()) 

这里将使用 Delaunay 三角剖分在内部生成一个三角形网格。因此，即使是完全随机的点也会产生不错的效果，如下图所示，这与给予的相同随机点进行了比较contour。

（这是生成此图片的代码）

解决方案 2：

后面算法的实际代码可以在_countour.cppplt.contour中找到。这是相当复杂的 C 代码，因此很难准确理解，但如果我试图编写一些轮廓生成代码，我会按照以下方式进行。选择边界上的某个点并固定其- 值。迭代附近的点，并选择 z 值最接近第一个点的 z 值的点。继续迭代新的点，选择 z 值最接近所需值的附近点（但请检查您不会返回到刚刚访问过的点，因此您必须朝某个“方向”前进），并继续，直到您获得一个循环或到达某个边界。(x, y)`z`

似乎在中实现了一些接近的东西（但稍微复杂一些）_counter.cpp。

从算法的非正式描述中可以看出，要继续进行，您必须找到一个“靠近”当前点的点。如果您有一个矩形点网格，这很容易做到（需要大约 4 或 8 次迭代，如下所示：(x[i+1][j], y[i+1][j])，，等等）。但是(x[i][j+1], y[i][j+1])，(x[i-1][j], y[i-1][j])如果您有一些随机选择的点（没有任何特定顺序），这个问题就会变得困难：您必须迭代所有点以找到附近的点并进行下一步。此步骤的复杂性为 O(n)，其中n是点数（通常是图片大小的正方形）。因此，如果您没有矩形网格，算法会变得慢​​得多。

这就是为什么您实际上需要三个二维数组来对应某个矩形网格上某些点的 x、y 和 z。

正如您正确提到的，x和y可以是一维数组。在这种情况下，相应的二维数组用 重建meshgrid。但是，在这种情况下，无论如何您都必须拥有z二维数组。

如果仅z指定，x并且y具有range适当长度。

编辑。您可以尝试“伪造”二维x、y和z数组，使得x和y不形成矩形网格，以检查我的假设是否正确。

import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

x = np.random.uniform(-3, 3, size=10000)
y = np.random.uniform(-3, 3, size=10000)
z = x**2 + y**2
X, Y, Z = (u.reshape(100, 100) for u in (x, y, z))
plt.contour(X, Y, Z)

如您所见，如果 (x, y, z) 只是一些随机点，那么该图片看起来并不像正确的图形。

现在让我们假设对x进行排序作为预处理步骤，正如@dhrummel 在评论中所建议的那样。请注意，我们不能同时对x和y进行排序，因为它们不是独立的（我们希望保留相同的点）。

x = np.random.uniform(-3, 3, size=10000)
y = np.random.uniform(-3, 3, size=10000)
z = x**2 + y**2
xyz = np.array([x, y, z]).T
x, y, z = xyz[xyz[:, 0].argsort()].T
assert (x == np.sort(x)).all()
X, Y, Z = (u.reshape(100, 100) for u in (x, y, z))
plt.contour(X, Y, Z)

再次，该图片是不正确的，因为y's 没有被排序（在每一列中），就像我们有矩形网格而不是一些随机点一样。

解决方案 3：

假设您要绘制一个三维图形。您有一组x点和一组y点。目标是z为每对x和生成一个值y，换句话说，您需要一个函数，f使其生成一个值，z以便z = f(x, y)。

这是一个很好的例子（取自 MathWorks）：

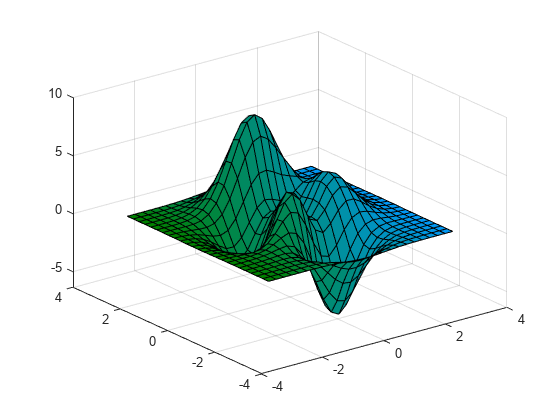
和坐标分别位于右下角和左下角。您将拥有一个函数，对于每一对和，我们都会生成一个值。因此，在您提供的代码中，调用将生成两个 2D 数组x，这样对于每个唯一的空间位置，我们将观察到该位置独有的和值。y`fxyznumpy.meshgridxy`

例如，我们使用一个很小的例子：

In [1]: import numpy as np

In [2]: x, y = np.meshgrid(np.linspace(-1, 1, 3), np.linspace(-1, 1, 3))
In [3]: x
Out[3]:
array([[-1.,  0.,  1.],
       [-1.,  0.,  1.],
       [-1.,  0.,  1.]])

In [4]: y
Out[4]:
array([[-1., -1., -1.],
       [ 0.,  0.,  0.],
       [ 1.,  1.,  1.]])

例如，看看行号 2 和列号 1（顺便说一下，我从 0 开始索引）。这意味着在这个空间位置，我们将有坐标x = 0.和y = 1。 numpy.meshgrid为我们提供了生成该特定坐标处的值所需的x和对。它只是为了方便起见，分成了两个二维数组。y`z`

现在，最终要在z变量中放入的是，它应该使用函数并处理每个值及其对应的f输出。x`y`

明确地，您需要制定一个z二维数组，使得：

z = [f(-1, -1) f(0, -1) f(1, -1)]
    [f(-1,  0) f(0,  0) f(1,  0)]
    [f(-1,  1) f(0,  1) f(1,  1)]

x仔细观察和项的空间排列y。我们为每对x和y值生成 9 个唯一值。x值的范围从 -1 到 1，并且 的值相同y。一旦为 生成此 2D 数组z，您就可以使用它contourf来绘制水平集，以便每条轮廓线都会为您提供所有可能的x和y值的集合，这些值等于 的相同值z。此外，在每对相邻的不同线之间，我们用相同的颜色填充中间的区域。

让我们用一个实际的例子来结束本文。假设我们有函数f(x, y) = exp(-(x**2 + y**2) / 10)。这是一个二维高斯函数，标准差为sqrt(5)。

因此，让我们生成一个x和y值的网格，并使用它来生成z值并绘制一个contourf图：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 101)
y = x
x, y = np.meshgrid(x, y)
z = np.exp(-(x**2 + y**2) / 10)       
fig,ax2 = plt.subplots(1)    
ax2.contourf(x,y,z)
plt.show()

我们得到：

解决方案 4：

X 和 Y 是二维的原因如下。Z 与轴系统中的每个 (x,y) 坐标匹配相应的“深度”，以创建具有 x、y 和 z 坐标的三维图。

现在假设我们想要指向轴系统内的任意点。我们可以通过提供该点的 x 和 y 坐标 (x,y) 来实现。例如 (0,0)。现在考虑 x 值为 1 的“线”。这条线上有许多 ny 值，看起来像：

如果我们为所有 x 值和 y 值绘制这条线，我们将得到如下结果：

如您所见，我们有一个由两个二维数组组成的二维注释，其中一个数组用于 x 值，其形状为：

1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10
#--> Two dimensional x values array

另一个用于 y 值，其形状如下：

10 10 10 10 10 10 10 10 10 10
9 9 9 9 9 9 9 9 9 9 
8 8 8 8 8 8 8 8 8 8
...
1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0
#--> Two dimensional y values array

这两个一起提供了坐标系中每个点的 (x,y) 坐标。现在我们可以为每个点绘制“深度”表示 Z 值（z 坐标）。现在也很明显为什么 Z 变量必须是具有形状 (len(x),len(y)) 的二维变量，因为否则它无法为所有点提供值。

此行为可以通过向函数提供 2D x、y 和 z 数组来实现，或者：向函数提供 1D x 和 y 数组，函数内部使用 x 和 y 值创建 2D 网格。如 X,Y=np.meshgrid(x,y)，但 z 必须是二维的。

解决方案 5：

让我用简单的方式解释一下，因为我认为 Z 也不应该是二维的。contourf()需要 X 和 Y 来构建自己的空间，需要关系 Z(X,Y) 来构建一个完整的空间，而不是仅仅使用几个具有一维 X、Y、Z 信息的点。